刷题记录

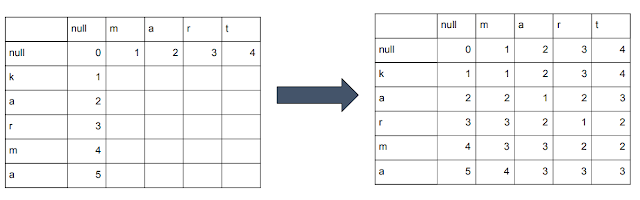
Problem: Given two strings, find the longest common subsequence ( LCS ). Your code should return the length of  LCS . Have you met this question in a real interview?   Yes Clarification What's the definition of Longest Common Subsequence? https://en.wikipedia.org/wiki/Longest_common_subsequence_problem http://baike.baidu.com/view/2020307.htm Example For  "ABCD"  and  "EDCA" , the  LCS  is  "A"  (or  "D" ,  "C" ), return  1 . For  "ABCD"  and  "EACB" , the  LCS  is  "AC" , return  2 . Analysis: 4/6/2018 update: if A[i - 1] != B[j - 1], why do we need to consider deleting A[i - 1]  and B[j - 1] separately?  It is common sense that the max LCS will be the max of dp[i - 1][j] and dp[i][j-1]. What else choice do we have! 思路 ： 匹配DP画矩阵 state : dp[i][j], 第一个string 前i个和第二个string 前j个的LCS. transition :  if(A[i-1]==B[j-1]) dp[i][j]=dp[...

Problem: Given two words  word1  and  word2 , find the minimum number of steps required to convert  word1  to  word2 . (each operation is counted as 1 step.) You have the following 3 operations permitted on a word: a) Insert a character b) Delete a character c) Replace a character 3/28/2018 update Solution: class Solution { public int minDistance ( String word1, String word2) { int m = word1 . length(); int n = word2 . length(); int [][] dp = new int [m + 1 ][n + 1 ]; for ( int i = 0 ; i <= n; i ++ ) { dp[ 0 ][i] = i; } for ( int i = 0 ; i <= m; i ++ ) { dp[i][ 0 ] = i; } for ( int i = 1 ; i <= m; i ++ ) for ( int j = 1 ; j <= n; j ++ ) { if (word1 . charAt(i - 1 ) == word2 . charAt(j - 1 )) { dp[i][j] = dp[i - 1 ][j - 1 ]; } else { ...

思路 ： 满足条件有2种情况 1. s1前i个和s2前i个是scramble string, s1后len-i个和s2后len-i个是scramble string 2. s1前i个和s2后i个是scramble string, s1后len-i个和s2前len-i个是scramble string 可以用递归来做: if(isScramble(s1.substring(0,i),s2.substring(0,i))&& isScramble(s1.substring(i),s2.substring(i))) return true; if(isScramble(s1.substring(0,i),s2.substring(s2.length()-i))&& isScramble(s1.substring(i),s2.substring(0,s2.length()-i))) return true; 实现： 有一个巧妙的方式来判断在2个string长度一样的时候是否字符都匹配。如下： int[] letters=new int[26]; for(int i=0;i<s1.length();i++) { letters[s1.charAt(i)-'a']++; letters[s2.charAt(i)-'a']--; } for(int i=0;i<26;i++) { if(letters[i]!=0) return false; }

思路 ： 几乎和stone game一模一样。因为允许circle，所以在这里扩展一次数组。比如[4,4,5,9]，就变成了[4,4,5,9,4,4,5,9]。区间还是1~n。 实现 ： 所求得的最终结果是每个区间的最小值。

思路： 一开始以为是stone game的马甲，结果情况更复杂。 transition : dp[i][j]=Max(dp[i][k-1]+dp[k+1][j]+nums[i-1]*nums[k]*nums[j+1])， i<=k<=j。dp[i][j]表示在i到j这个区间(inclusive)打气球得到的最大值。而k表示，最后一个打第k个气球的情况。比如[4,1,5,5]，最后一个打1，那么[4]和[5,5]都打完了，打1的时候的值就是1*1*1，不包括边界(exclusive)。 实现细节： 这里需要把第-1个和第n+1个2个为1的气球放进数组里。所以需要一个新的长度为n+2的数组。

思路： state: dp[i][j]代表从第i个石头到第j个石头，能堆的最小cost。 transition: dp[i][j]=min(dp[i][k]+dp[k+1][j]+sum[i][j]), i<=k<j。s[i][j]是拆分后最后一步需要的cost。 initial value: dp[i][i]=0 实现细节：取最小值循环前，应该赋给当前dp最大值。

虽然是hard，但是真正理解起来并不难。关键是要知道区间dp的概念。因为棋手是前后端都可以选，单个状态dp不好表示，所以利用区间dp[i][j]表示在i->j这个区间先手能取到的最大值。 dp[i][j]=sum[i][j]-min(dp[i][j-1],dp[i+1][j])。这道题用记忆化搜索的递归方法来实现。

一开始想用O(n)来做，结果是错的。要用两层循环DP来做。假设当前index 为i，在0<j<i-1中。如果nums[i]>nums[j]， dp[i]=max(dp[j])+1。dp[i]很不好理解，其实dp[n-1]并不是所求的结果，而是以nums[i]为最大值，的longest increasing subsequence。看了2个小时，终于把这一点看懂了。leetcode article 没说清楚啊。

Problem: Find the contiguous subarray within an array (containing at least one number) which has the largest product. For example, given the array  [2,3,-2,4] , the contiguous subarray  [2,3]  has the largest product =  6 . Analysis: 2/26/2018 update: Similar to Maximum subarray. Since the array may contain negative number, we need to keep track of minSoFar and maxSoFar. If current number is negative, we swap min and max. Solution: class Solution { public int maxProduct ( int [] nums) { if (nums == null || nums . length == 0 ) return Integer . MIN_VALUE; int min = nums[ 0 ], max = nums[ 0 ], res = nums[ 0 ]; for ( int i = 1 ; i < nums . length; i ++ ) { if (nums[i] < 0 ) { int temp = min; min = max; max = temp; } min = Math . min(nums[i], min * nums[i]); max = Math . max(nums[i], max * ...

Problem: Find the contiguous subarray within an array (containing at least one number) which has the largest sum. For example, given the array  [-2,1,-3,4,-1,2,1,-5,4] , the contiguous subarray  [4,-1,2,1]  has the largest sum =  6 . 3/29/2018 update: 更新maxEndingHere在sum[0, i - 1] 小于0的情况下，如果当前nums[i] > 0,肯定要把之前的都抛弃。maxEndingHere不一定是包含了0 ~ i所有的数。 相当于维护一个当前的极大和，因为是求subarray，所以最大和肯定是极大和的最大值。 2/23/2018 update DP solution:  maxEndingHere  is the max sum from  nums[0] to nums[i] that includes nums[i]. public static int maxSubArray( int [] A ) { int maxSoFar = A [ 0 ], maxEndingHere = A [ 0 ]; for ( int i = 1 ;i < A . length; ++ i){ maxEndingHere = Math . max(maxEndingHere + A [i], A [i]); maxSoFar = Math . max(maxSoFar, maxEndingHere); } return maxSoFar; } 10/10/2017 第二种解法用prefix sum的思路来做。 前i个数的maximum subarray = prefixSum[i] - min(prefixSum[0]....prefixSum[i-1])。 在遍历数组的时候需要记录下minSum, s...

简单题，太直接了。不需要用DP,否则空间复杂度太高。实现可以只用一个循环。

个人认为这到题不太适合用记忆化搜索。记忆化搜索枚举太多不容易想出来，而且实现比较复杂，容易错。 dp[i]表示还剩i个棋子，当前取的人所获得的最大价值。如果i==3, 先手就有2种情况，取1个或者取2个棋子都是dp[3]。对手就会对应的取dp[1]或者dp[2]价值的棋子。然后dp[3]可以Max(sum[3]-dp[1],sum[3]-dp[2])来获得。sum[i]代表后i个棋子的总和。有了d[2]和dp[3]，就可以求得dp[4]，一直到dp[n]。 实现的时候必须初始化dp[2]，因为dp数组长度是n+1, dp[2]可以通过dp[0]和dp[1]求出来。

dp[i]表示还剩i个棋子的时候取的那个人的输赢。要让dp[i]赢，那么dp[i-1]和dp[i-2]至少有一个需要输。因为前一个状态输了，就是对手最后取。现在就轮到先手的人取了，必赢。实现的时候要注意dp数组长度是n+1.

记忆化搜索。 1. 不能赋初始值，因为dp[0][0]有可能成为终点，走的方向是上下左右。 2. 实现的时候在search函数里面，要把求得的值赋给dp[x][y]。因为如果在search里面调用search，"res=Math.max(res,search(newx,newy,A)+1);",这里求得的结果其实是dp[x][y],如果不赋值给dp[x][y]，那么就白调用了。

和maximal square类似，只不过对于 上面和左边不是看有多少1，而且看在对角点这个范围内是否有1,有1 则不满足，dp[j]=1。否则dp[j]=1+prev。检查左和上1的时候注意是否越界。

挨个遍历，当前位置作为正方形右下角。当前位置正方形边长最大取决于，上，左上，和左为有下点边长最小的。f[i][j] 表示以i和j作为正方形右下角可以拓展的最大边长。状态转换式为：f[i][j] = min(f[i - 1][j], f[i][j-1], f[i-1][j-1]) + 1。 这道题空间可以优化，用滚动数组在实现。行变为滚动数组。 九章上面的答案比较复杂，leetcode article 官方答案更简洁。把dp矩阵多留一行和一列，就不用考虑初始化dp[0][j]和dp[i][0]的问题了。 https://leetcode.com/articles/maximal-square/#approach-3-better-dynamic-programming-accepted public class Solution { public int maximalSquare(char[][] matrix) { int rows = matrix.length, cols = rows > 0 ? matrix[0].length : 0; int[][] dp = new int[rows + 1][cols + 1]; int maxsqlen = 0; for (int i = 1; i <= rows; i++) { for (int j = 1; j <= cols; j++) { if (matrix[i-1][j-1] == '1'){ dp[i][j] = Math.min(Math.min(dp[i][j - 1], dp[i - 1][j]), dp[i - 1][j - 1]) + 1; maxsqlen = Math.max(maxsqlen, dp[i][j]); } } } return maxsqlen * maxsqlen; } } 下面的代码是空间优化后的： public class Solution { ...

Problem: Note:  This is an extension of  House Robber . After robbing those houses on that street, the thief has found himself a new place for his thievery so that he will not get too much attention. This time, all houses at this place are  arranged in a circle.  That means the first house is the neighbor of the last one. Meanwhile, the security system for these houses remain the same as for those in the previous street. Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight  without alerting the police . Analysis: 把first 和last element分别去掉求house robber。然后取2个house robber的最大值。实现houseRobber花了点时间，因为start和end是动态的。记住一点就好，在循环里面F[i%2]的第一个肯定是i%2==0。这样一开始的i就必须是2，不能是动态的。 Solution: 第二遍实现感觉编码能力提升太多。 class Solution { public int rob ( int [] nums) { if (nums == null || nums . length == 0 ) return 0 ; if (nums . length() == 1 ) retu...

序列型动态规划 • 状态 State • f[i] 表示前i个房子中，偷到的最大价值 •方程 Function • f[i] = 1. A[i-1] + max(f[i-2]....f[1]) 偷第i个房子            2. f[i-1] 不偷第i个房子 总结为 • f[i] = max(f[i-1], f[i-2] + A[i-1]); • 初始化 Intialization    f[0] = 0;    f[1] = A[0]; • 答案 Answer • f[n] 这里节省空间可以用滚动数组，只需要大小为2的数组就行。下图是一个滚动数组的演示。

这属于sweep line问题，一开始我想到把所有边放到堆里排序这没问题。但在取出来的时候没有用合适的数据结构，造成了判断end point的情况特别复杂。如果自己觉得情况很复杂的时候，多半是方向错了。从左到右扫描的时候用的是max heap来帮助找到高度变化的点,因为当前建筑的高度是最高点决定的,自动过滤到新进来的比最高点小的起点。遇到end就删除相应的start。 高度变化有2种情况： 1.升高，新的start比现有最高点高。把新的高度加入heap. 2.下降，现在这个高度达到end,heap里面高度为空。 lintcode需要求start,end,height，增加了程序的复杂度。end有两种情况： 1.start变了也就是cur height!= heap top. 2.end后面就是陆地高度为零。这个时候heap里面没有存任何高度。 heap.peek()==0 实现方面，可以用一个int[2]代替Point 类。把start point的高度设置为负。虽然代码量减少了，但是可读性也下降了。不建议这样做，还是老老实实写Point 类。 from left to right { if(start edege) add height to heap else remove height from heap //pre!=null 要排除pre前面是陆地的情况 if(heap top ==0 or cur height != heap top) { if(pre!=null && pre height != cur height) add range(pre to cur) to result if(top==0) { pre= null } else pre=cur } }

把起飞和降落看成括号就好理解了。比如(())()，左括号就是起飞（1），又括号就是降落（-1）。从左到右挨着遍历，算出遍历中的最大值。实现的难点在于comparator, 如果起飞降落在同一时间则可以用 return p1.flag-p2.flag表示。结果小于零则p1在前，大于零则p2在前。

1. How to determine return value of BS? end or start? 2. 如何确定start的启示值？0 或是1 3. Maximum Average Subarry II，看不懂啊看不懂需要debug一步一步来。 4. 记忆化DP时间复杂度分析。 5. backpack 4方法2看不懂。为什么从小到大就能表示重复的。 6. Knight's shortest path 标记问题。 7. quickselect find kth smallest, 为什么往左往右都找kth. 8. longest substring without duplicates: 如何想到在更新i时比较当前的i. 9. Merge list condition head.next != null 10. Why is binary tree bottom up approach bottom up? 11. 为什么新二分法模板hi = nums.length (search for a range) 12. Remove invalid parentheses 的last_j是什么意思，一直没看懂啊。。。。

Problem: Given n pieces of wood with length  L[i]  (integer array). Cut them into small pieces to guarantee you could have equal or more than k pieces with the same length. What is the longest length you can get from the n pieces of wood? Given L & k, return the maximum length of the small pieces.  Notice You couldn't cut wood into float length. If you couldn't get >=  k  pieces, return  0 . Analysis: Binary search, guess the result. If guess value (cut by assumed wood length) >= k, then increase the guess value. Solution: Start always satisfy the requirement, so just return start. public class Solution { /* * @param L: Given n pieces of wood with length L[i] * @param k: An integer * @return: The maximum length of the small pieces */ public int woodCut ( int [] L , int k) { // write your code here if ( L == null || L . length == 0 ) return 0 ; int start = 0 , end ...

why end<1.0? then end=1. if so, mid*mid will always less than x. then result will be very close to x. but the actual result is lager then x.

Problem: Implement  int sqrt(int x) . Compute and return the square root of  x , where  x  is guaranteed to be a non-negative integer. Since the return type is an integer, the decimal digits are truncated and only the integer part of the result is returned. Example 1: Input: 4 Output: 2 Example 2: Input: 8 Output: 2 Explanation: The square root of 8 is 2.82842..., and since   the decimal part is truncated, 2 is returned. Analysis: The qualified square root satisfies that root*root <= x. So need to cache result under smaller and equal condition. Solution: class Solution { public int mySqrt ( int x) { if (x == 0 ) return 0 ; int low = 1 , high = x, res = 1 ; while (low < high) { int mid = low + (high - low) / 2 ; if (mid <= x / mid) { low = mid + 1 ; res = mid; } else high = mid...

Problem: A peak element is an element that is greater than its neighbors. Given an input array where  num[i] ≠ num[i+1] , find a peak element and return its index. The array may contain multiple peaks, in that case return the index to any one of the peaks is fine. You may imagine that  num[-1] = num[n] = -∞ . For example, in array  [1, 2, 3, 1] , 3 is a peak element and your function should return the index number 2. Analysis: if (nums[m - 1] < nums[m] < nums[m+1]) peak is on right if (nums[m - 1] > nums[m] > nums[m+1]） peak is on left Solution： Return whichever is larger.  class Solution { public int findPeakElement ( int [] nums) { int left = 0 , right = nums . length - 1 ; while (left + 1 < right) { int mid = left + (right - left) / 2 ; if (nums[mid] > nums[mid + 1 ]){ right = mid; } else { left = mid; ...

Problem: Given  n  non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram. Above is a histogram where width of each bar is 1, given height =  [2,1,5,6,2,3] . The largest rectangle is shown in the shaded area, which has area =  10  unit. 5/30/2018 update: The stack only pops out which ever is shorter than current height.  Why do we calc width from stack.peek instead of using the position of current height? For instance, the above histogram. When reach end, the stack contains [3,2,1], when 2 is being popped. The actual width is from pos 2 to 5. 1 is stack top.  --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- - Analysis: Detailed illustration from here  http://www.cnblogs....

PriorityQueue<Node> queue=new PriorityQueue<Node>(k,new Comparator<Node>(){             public int compare(Node a, Node b)             {                 return a.sum-b.sum;             }         });

Problem: Given a 2D board and a list of words from the dictionary, find all words in the board. Each word must be constructed from letters of sequentially adjacent cell, where "adjacent" cells are those horizontally or vertically neighboring. The same letter cell may not be used more than once in a word. For example, Given  words  =  ["oath","pea","eat","rain"]  and  board  = [ [' o ',' a ','a','n'], ['e',' t ',' a ',' e '], ['i',' h ','k','r'], ['i','f','l','v'] ] Return  ["eat","oath"] . Analysis: 6/6/3028 update: 这道题的思想很简答，但是写成bug free各种情况都考虑到很难。这一遍保存word考虑到了，去重没想到。 ------------------- ------------------- ------------------- ------------------- ------------------- ------------------- ------------------- ------- 3/6/0218 update: The problem is how to validate the ...

Problem： Design a data structure that supports the following two operations: void addWord(word) bool search(word) search(word) can search a literal word or a regular expression string containing only letters  a-z  or  . . A  .  means it can represent any one letter. For example: addWord("bad") addWord("dad") addWord("mad") search("pad") -> false search("bad") -> true search(".ad") -> true search("b..") -> true 6/5/2018 update: 这次是自己想出来的如何处理‘.’。有.时候，需要遍历当前trienode所有的children。所以用递归比较好实现。 TrieNode的children用hashmap更方便。而且居然自己想出来如何处理，for循环里面boolean结果的方法，感觉快出山了。 class WordDictionary { class TrieNode { Map< Character , TrieNode > children; boolean isWord; public TrieNode () { children = new HashMap<> (); } } TrieNode root; /** Initialize your data structure here. */ public WordDictionary () { root = new Tri...

Problem: Implement a trie with  insert ,  search , and  startsWith  methods. 6/5/2018 update: 现在倾向于用hash map来表示children. class TrieNode { Map< Character , TrieNode > children; boolean isWord; public TrieNode () { children = new HashMap<> (); } } TrieNode root; /** Initialize your data structure here. */ public WordDictionary() { root = new TrieNode (); } /** Adds a word into the data structure. */ public void addWord( String word) { TrieNode cur = root; for ( char c : word . toCharArray()) { if ( ! cur . children . containsKey(c)) { cur . children . put(c, new TrieNode ()); } cur = cur . children . get(c); } cur . isWord = true; } -------- -------- -------- -------- -------- -------- -------- -------- -------- -------- -------- -------- -------- -----...