Edit Distance
Problem:
思路:
匹配类动态规划,需要画矩阵来分析。
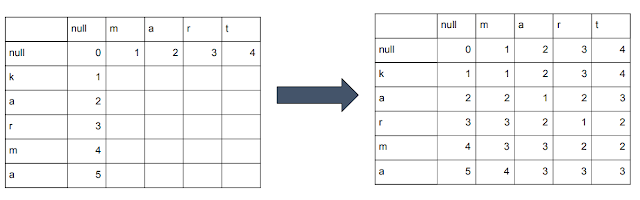
dp[i][j]表示word1前i个转换到word2前j个需要的最小步骤。dp[i][j]通过3种情况得到的。
1.dp[i-1][j], 需要删除i,因为i-1已经可以到j了,所以i是多余的需要删除,这里操作步骤为1,
dp[i][j]=dp[i-1][j]+1. karm->mart 需要2次,karma到->mart删除a就行了。
2.dp[i][j-1], i能到j-1, 为了到j再加一个word2 charAt(j)就好了。所以dp[i][j]=d[i][j-1]+1.
karma->mar需要3次,karma->mart加上t就行了。
3. dp[i-1][j-1],这种情况最好理解,如果word1[i]==word2[j],不做任何操作,否则做一次替换操作。
Transition: dp[i][j]=min(dp[i-1][j]+1,dp[i][j-1]+1, word1.charAt(i-1)==word2.charAt(j-1)?
dp[i-1][j-1]:
dp[i-1][j-1]+1,dp[i][j]);
Given two words word1 and word2, find the minimum number of steps required to convert word1 to word2. (each operation is counted as 1 step.)
You have the following 3 operations permitted on a word:
a) Insert a character
b) Delete a character
c) Replace a character
b) Delete a character
c) Replace a character
3/28/2018 update
Solution:
class Solution { public int minDistance(String word1, String word2) { int m = word1.length(); int n = word2.length(); int[][] dp = new int[m + 1][n + 1]; for (int i = 0; i <= n; i++) { dp[0][i] = i; } for (int i = 0; i <= m; i++) { dp[i][0] = i; } for (int i = 1; i <= m; i++) for (int j = 1; j <= n; j++) { if (word1.charAt(i -1) == word2.charAt(j - 1)) { dp[i][j] = dp[i - 1][j - 1]; } else { dp[i][j] = Math.min(dp[i - 1][j],
Math.min(dp[i][j - 1], dp[i - 1][j - 1])) + 1; } } return dp[m][n]; } }
匹配类动态规划,需要画矩阵来分析。

dp[i][j]表示word1前i个转换到word2前j个需要的最小步骤。dp[i][j]通过3种情况得到的。
1.dp[i-1][j], 需要删除i,因为i-1已经可以到j了,所以i是多余的需要删除,这里操作步骤为1,
dp[i][j]=dp[i-1][j]+1. karm->mart 需要2次,karma到->mart删除a就行了。
2.dp[i][j-1], i能到j-1, 为了到j再加一个word2 charAt(j)就好了。所以dp[i][j]=d[i][j-1]+1.
karma->mar需要3次,karma->mart加上t就行了。
3. dp[i-1][j-1],这种情况最好理解,如果word1[i]==word2[j],不做任何操作,否则做一次替换操作。
Transition: dp[i][j]=min(dp[i-1][j]+1,dp[i][j-1]+1, word1.charAt(i-1)==word2.charAt(j-1)?
dp[i-1][j-1]:
dp[i-1][j-1]+1,dp[i][j]);
评论
发表评论