204. Count Primes
Problem:
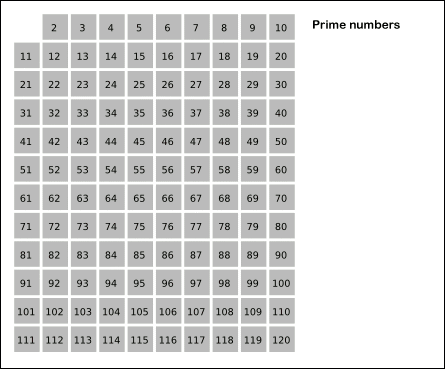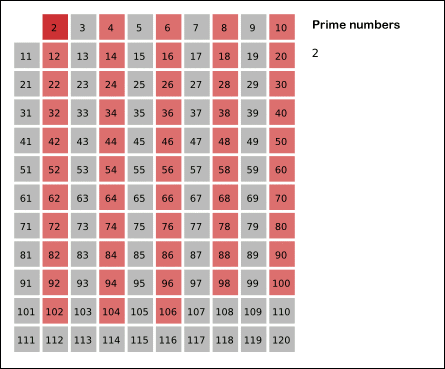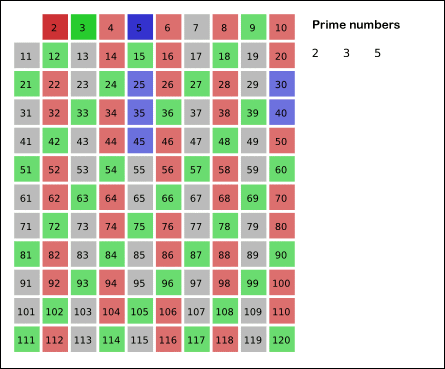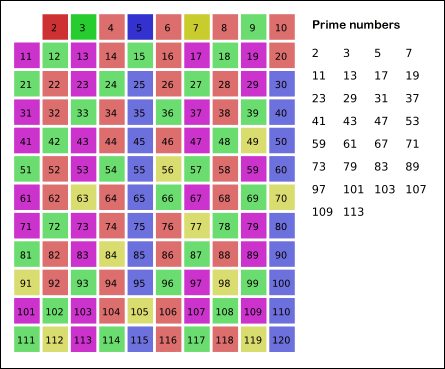
Sieve of Eratosthenes: algorithm steps for primes below 121. "Sieve of Eratosthenes Animation" by SKopp is licensed under CC BY 2.0.
Count the number of prime numbers less than a non-negative number, n.
Example:
Input: 10 Output: 4 Explanation: There are 4 prime numbers less than 10, they are 2, 3, 5, 7.
7/2/2018 update
A shorter solution:
Analysis:
A shorter solution:
class Solution { public int countPrimes(int n) { boolean[] notPrime = new boolean[n]; int count = 0; for (int i = 2; i < n; i++) { if (!notPrime[i]) { count++; for (int j = 2; i*j < n; j++) { notPrime[i*j] = true; } } } return count; } }--------------------------------------------------------------------------------------------------------------------------------------------
Analysis:
The Sieve of Eratosthenes is one of the most efficient ways to find all prime numbers up to n. But don't let that name scare you, I promise that the concept is surprisingly simple.

Sieve of Eratosthenes: algorithm steps for primes below 121. "Sieve of Eratosthenes Animation" by SKopp is licensed under CC BY 2.0.
Mark none prime number from the process above. 遍历的数i应该小于根号n, 避免重复计算。
Solution:
class Solution { public int countPrimes(int n) { boolean[] isPrime = new boolean[n]; for (int i = 2; i < n; i++) { isPrime[i] = true; } for (int i = 2; i*i < n; i++) { if (isPrime[i]) { for (int j = i*i; j < n; j += i) { isPrime[j] = false; } } } int count = 0; for (int i = 0; i < n; i++) { if(isPrime[i]) count++; } return count; } }
评论
发表评论