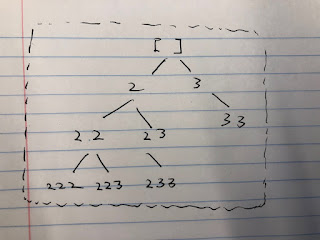刷题记录

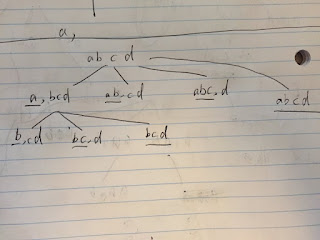
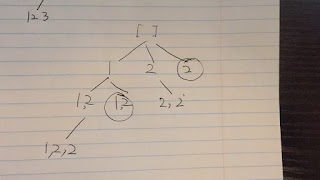
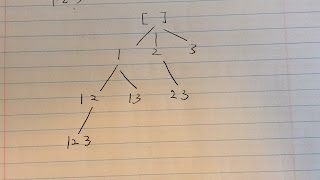
Problem: Given a collection of numbers that might contain duplicates, return all possible unique permutations. Example: Input: [1,1,2] Output: [ [1,1,2], [1,2,1], [2,1,1] ] Analysis: 5/28/2018 Since each for loop the valid number might not start from index 0, if the nums[i - 1] has been used(the upper level), and nums[i] == nums[i -1], we can use nums[i]. --------------------------------- --------------------------------- --------------------------------- ---------------------- 1/23/2018 The numbers on the same level are not used, cuz the used mark will be removed after backtracking. So the used[i - 1] checks whether nums[i - 1] has been used at upper level. Solution: class Solution { public List< List< Integer > > permuteUnique ( int [] nums) { List< List< Integer > > res = new ArrayList<> (); if (nums == null || nums . length == 0 ) { return null; } Arrays . sort(nums);...

3/27/2018 update: 用index肯定比用substring 要快。 1/22/2018 Solution: class Solution { public List< List< String > > partition ( String s) { List< List< String > > res = new ArrayList<> (); if (s == null || s . length() == 0 ) return null; helper(res, new ArrayList<> (), s); return res; } private void helper ( List< List< String > > res, List< String > temp, String s) { if (s . length() == 0 ) { res . add( new ArrayList<> (temp)); return ; } for ( int i = 0 ; i < s . length(); i ++ ) { if (isPalindrome(s . substring( 0 , i + 1 ))) { temp . add(s . substring( 0 , i + 1 )); helper(res, temp, s . substring(i + 1 )); temp . remove(temp . size() - 1 ); } } } private boolean isPalindrome ( Stri...

Problem: Given a collection of candidate numbers ( C ) and a target number ( T ), find all unique combinations in  C  where the candidate numbers sums to  T . Each number in  C  may only be used  once  in the combination. Note: All numbers (including target) will be positive integers. The solution set must not contain duplicate combinations. For example, given candidate set  [10, 1, 2, 7, 6, 1, 5]  and target  8 , A solution set is:  [ [1, 7], [1, 2, 5], [2, 6], [1, 1, 6] ] 3/26/2018 update: 第三遍写还是有问题。忘记了排序，index 忘记了 + 1. 思路： 和combination sum几乎一模一样。不允许重复那么就是startIndex = i+1。在for循环里面需要去除重复，也就是在树的同一层不能出现重复的数，否则答案会重复。其中一个判断条件是i != startIndex 而不是 i != 0。如果用i != 0 , [1,1,2] t =4, 这个例子就没有答案。直接把深度上重复的数给忽略了。 combination sum是数组里面不允许重复，II是在树的同一层不允许重复。 for循环一次其实就是铺开树的一层。

1/22/2018 The provided array has no duplicate, so no need to remove duplicate. The solution set won't have duplicates as the tree expands. Solution: class Solution { public List< List< Integer > > combinationSum ( int [] candidates, int target) { // write your code here List< List< Integer > > res = new ArrayList<> (); if (candidates == null) { return null; } //Arrays.sort(candidates); List< Integer > subset = new ArrayList< Integer > (); Arrays . sort(candidates); search(subset, 0 , res, candidates, target); return res; } private void search ( List< Integer > subset, int startIndex, List< List< Integer > > res, int [] candidates, int remain) { if (remain == 0 ) { res . add( new ArrayList<> (subset)); return ; } fo...

思路： 一开始的做法是最直接的: 从每一个emtpy开始BFS， 访问所有house, 记录下distance。然后再找到最小distance。很可惜超时了。 九章答案的做法是：以每一个house为起点做BFS， 记录下每一个empty到该house的距离。同时记录每一个empty点到所有house的距离。找出最小的距离就行了。 做完这道题感觉自己BFS基本过关了。 实现： 要合理利用coordinate类， 在找所有house和所有empty点操作其实是重复的，为何不单独开一个函数来处理？ private List<Coordinate> getCoordinates(int type) { List<Coordinate> coordinates = new ArrayList<>(); for (int i = 0; i < n; i++) { for (int j = 0; j < m; j++) { if (grid[i][j] == type) { coordinates.add(new Coordinate(i, j)); } } } return coordinates; }

思路： 这道题和search graph node类似，不要一看到shortest 或者 closest 就被吓到了， 然后就开始比较。BFS的优势就在于，搜索过程中，最先到达满足条件的点的path就是最近的。 实现： 因为是path, 所以每访问一个点就要标记true， 不能再访问了。但是其实这种标记方法是有问题的。在当前point 往下走过的标记了true, 但是并不代表其他路径不能进过这个点啊。

思路： 典型的拓扑排序。 实现： 一看到这种给n个点，点是从0到n-1，就要考虑一维数组节省空间。那么可以定义 List[] edges =  new ArrayList[numCourses]; int[] degrees = new int[numCourses]; 找degree和edge的方法很简单。 每一次从edges里面取出点一定先要把入度递减1。是因为这一条edge已经遍历过了。 在BFS的时候需要一个incremented index来不断给结果数组赋值。代码如下： public class Solution { /* * @param numCourses: a total of n courses * @param prerequisites: a list of prerequisite pairs * @return: the course order */ public int[] findOrder(int numCourses, int[][] prerequisites) { // write your code here List[] edges = new ArrayList[numCourses]; int[] degrees = new int[numCourses]; for (int i = 0;i < numCourses; i++) edges[i] = new ArrayList<Integer>(); for(int i = 0; i < prerequisites.length; i++) { degrees[prerequisites[i][0]]++; edges[prerequisites[i][1]].add(prerequisites[i][0]); } // get starting nodes. Queue<Integer> queue = new LinkedList<...

思路： 三部曲 1. indegree 把所有node的入度算出来，也就是有多少条边进入它。放进hashmap里面。 2. get start nodes 把所有入度为零的点找出来。 3. bfs 每一次进入下一层，把下一层节点的入度减1。 当节点入度为0的时候才加入到queue和result中。因为入度越高优先级就越高就越靠后。 实现： /** * Definition for Directed graph. * class DirectedGraphNode { * int label; * ArrayList<DirectedGraphNode> neighbors; * DirectedGraphNode(int x) { label = x; neighbors = new ArrayList<DirectedGraphNode>(); } * }; */ public class Solution { /* * @param graph: A list of Directed graph node * @return: Any topological order for the given graph. */ public ArrayList<DirectedGraphNode> topSort(ArrayList<DirectedGraphNode> graph) { // write your code here ArrayList<DirectedGraphNode> result = new ArrayList<>(); // 1. indegree Map<DirectedGraphNode, Integer> map = new HashMap<>(); for(DirectedGraphNode node: graph) { for(DirectedGraphNode neighbor...

思路： 比想象中的简单很多。因为只是找最近的而不是所有的target，在BFS过程中遇到的第一个target必然是最近的。然后给的graph 参数完全没用用到，影响了思路。 实现： 在判断当前node值是否是target时应该在内层循环外，不然初始node会被漏掉。

思路: 把每一层的node放进queue里面。在下次循环的时候把queue头取出来然后再把它的子节点放进queue里面。每一次循环queue里面的节点就是当前level的节点。 进去下一次的循环的时候，queue里面会有可能包含2个level的节点，所以要在内层循环里面加一个上一个level节点数size来控制queue.poll()的次数，也就是在只pop当前层的节点。 实现： 上面说了一堆其实看代码是最清晰的： /** * Definition of TreeNode: * public class TreeNode { * public int val; * public TreeNode left, right; * public TreeNode(int val) { * this.val = val; * this.left = this.right = null; * } * } */ public class Solution { /* * @param root: A Tree * @return: Level order a list of lists of integer */ public List<List<Integer>> levelOrder(TreeNode root) { // write your code here List<List<Integer>> result = new ArrayList<>(); if(root == null) return result; Queue<TreeNode> queue = new LinkedList<TreeNode>(); queue.add(root); while(!queue.isEmpty()) { List<Integer> curLvl = new Ar...

Problem: Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand. (i.e.,  [0,1,2,4,5,6,7]  might become  [4,5,6,7,0,1,2] ). You are given a target value to search. If found in the array return its index, otherwise return  -1 . You may assume no duplicate exists in the array. Your algorithm's runtime complexity must be in the order of  O (log  n ). Example 1: Input: nums = [ 4,5,6,7,0,1,2] , target = 0 Output: 4 Example 2: Input: nums = [ 4,5,6,7,0,1,2] , target = 3 Output: -1 Analysis: 6/19/2018 update: If mid value is on upper part, it's easier to control going left. So that target has to on the upper part: target >= nums[left]. and target needs to be smaller than mid value, target < nums[mid]. Same thing applies to lower part. The left and right points are inclusive. So add == to condition. No need to use start + 1 < end template, since this problem finds the exact value. class So...

Problem: Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand. (i.e.,   [0,1,2,4,5,6,7]  might become   [4,5,6,7,0,1,2] ). Find the minimum element. You may assume no duplicate exists in the array. Example 1: Input: [3,4,5,1,2] Output: 1 Example 2: Input: [4,5,6,7,0,1,2] Output: 0 Analysis: 6/19/2018 update: This problem finds minimum, so we can apply start + 1 < end template, since there is a standard, minimum, to check. -------------------------------- -------------------------------- -------------------------------- ------------------------- 01/18/2018 update Template 1 solution: class Solution { public int findMin ( int [] nums) { int start = 0 , end = nums . length - 1 ; while (start + 1 < end) { int mid = start + (end - start) / 2 ; if (nums[mid] > nums[end]){ start = mid; } else { ...

思路： 先要找到比target大的边界，可以用index*2一直找直到比target大，剩下的就是普通binary search了。 lintcode 这题有bug，我用的是i没有index，就超时。。。

01/18/2018 update Solution: public class Solution { /** * @param nums a mountain sequence which increase firstly and then decrease * @return then mountain top */ public int mountainSequence ( int [] nums) { // Write your code here if (nums == null || nums . length == 0 ) { return 0 ; } int start = 0 ; int end = nums . length - 1 ; while (start + 1 < end) { int mid = (start + end) / 2 ; if (nums[mid] > nums[mid + 1 ]) { end = mid; } else { start = mid; } } return Math . max(nums[start], nums[end]); } } ------------------------------------------------------------------------------------------------------------------------ 思路： 虽然写出来通过了，但是很复杂。九章的答案很简洁。直接比较nums[mid]>nums[mid+1]，如果成立则mountain在左边，否则mountain在右边。最后取nums[start] nums[end]最大的一个就好了。循环条件写成start+1 < end...

01/13/2018 update ---------------------- ---------------------- ---------------------- ---------------------- ---------------------- ------------ Why is high set to m*n  - 1 instead of m*n? If we set high to m*n, with [[1]]. mid would be 01/12/2018 update Refined template solution: class Solution { public boolean searchMatrix ( int [][] matrix, int target) { if (matrix . length == 0 || matrix == null || matrix[ 0 ] . length == 0 ) return false; int m = matrix . length; int n = matrix[ 0 ] . length; int low = 0 , high = m * n - 1 ; while (low < high) { int mid = low + (high - low) / 2 ; int midValue = matrix[mid / n][mid % n]; if (target == midValue) { return true; } else if (target > midValue){ low = mid + 1 ; } else { high = mid; } } return m...

思路： 在循环的时候只检查A[mid] == target, 退出循环后比较A[start]和A[end]和target的距离。

Problem: Given a binary tree, determine if it is a valid binary search tree (BST). Assume a BST is defined as follows: The left subtree of a node contains only nodes with keys  less than  the node's key. The right subtree of a node contains only nodes with keys  greater than  the node's key. Both the left and right subtrees must also be binary search trees. Example 1: Input: 2 / \ 1 3 Output: true Example 2: 5 / \ 1 4   / \   3 6 Output: false Explanation: The input is: [5,1,4,null,null,3,6]. The root node's value   is 5 but its right child's value is 4. Analysis: 5/30/2018 Update: The iterative inorder traversal approach is trivial. What is worth to know is the recursive divide and conquer approach. Details see code. Solution: class Solution { public boolean isValidBST ( TreeNode root) { return helper(root, Long . MIN_VALUE, Long . MAX_VALUE); } priva...

Problem: Given a binary tree, flatten it to a linked list in-place. For example, given the following tree: 1 / \ 2 5 / \ \ 3 4 6 The flattened tree should look like: 1 \ 2 \ 3 \ 4 \ 5 \ 6 4/30/2018 update: Analysis:  Divide and conquer. Flat left and right child trees first. Flattened left child tree is root's right. The flattened right child tree has to connect to the right most node of root and flattened left combined. Remember to set root's left to null. Solution: class Solution { public void flatten(TreeNode root) { if (root = = null) return ; if (root.left ! = null) flatten(root.left); if (root.right ! = null) flatten(root.right); TreeNode temp = root.right; root.right = root.left; root.left = null; while (root.right ! = null) { root = root.right; } root.right = temp; } }  ------...

思路： 这是minimum subtree的马甲。 实现： 需要定义一个result type { int sum, int size}。int做除法会有误差所以需要做特殊处理，除了subtree全局变量外还需要一个subtree result type来做全局变量。 更新max avg判断条件为： if(subtree == null || result.sum * subtreeRT.size > subtreeRT.sum * result.size)。

Problem: Given a binary tree, determine if it is height-balanced. For this problem, a height-balanced binary tree is defined as: a binary tree in which the depth of the two subtrees of  every  node never differ by more than 1. Example 1: Given the following tree  [3,9,20,null,null,15,7] : 3 / \ 9 20 / \ 15 7 Return true. Example 2: Given the following tree  [1,2,2,3,3,null,null,4,4] : 1 / \ 2 2 / \ 3 3 / \ 4 4 Return false. 12/29/2017 update Solution 1: Brute force, /** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */ class Solution { public boolean isBalanced(TreeNode root) { if (root == null) return true; return Math.abs(depth(root.left) - depth(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.r...

3/16/2018 update: Inorder and preorder should use the template as follows. Because the Binary Search Tree Iterator uses this template. public class Solution { public List < Integer > inorderTraversal ( TreeNode root) { List < Integer > res = new ArrayList < > (); Stack < TreeNode > stack = new Stack < > (); TreeNode curr = root; while (curr != null || ! stack . isEmpty()) { while (curr != null) { stack . push(curr); curr = curr . left; } curr = stack . pop(); res . add(curr . val); curr = curr . right; } return res; } } 2/24/218 update Preorder adds value when pushing, inorder adds value when popping. -------------------------------------------------------------------------------------------------- 1/9/2018 update Postorder iterative is too hard without reversing preorder. Need to memorize th...

思路： DC和traversal 结合。用全局变量记录临时的min sum和sub tree。

思路 ： D&C，很直接 实现 ： 在整合path的时候用到paths.add(root.val + "->" + path), 当root为叶节点的时候要单独处理。paths.add(""+root.val).

Problem: Given a binary tree, find its maximum depth. The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node. Note:  A leaf is a node with no children. Example: Given binary tree  [3,9,20,null,null,15,7] , 3 / \ 9 20 / \ 15 7 return its depth = 3. 4/21/2018 Analysis: 这道题比求mini depth 简单。 Solution: /** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */ class Solution { public int maxDepth ( TreeNode root) { if (root == null) return 0 ; int left = maxDepth(root . left) + 1 ; int right = maxDepth(root . right) + 1 ; return Math . max(left, right); } }

思路： 递归版太简单了。迭代版需要用到stack，由于preorder 是root-> left -> right。所以stack push的顺序是反的。先检查right 是否为空，push right, 再处理left。

Problem: Given a collection of integers that might contain duplicates,  nums , return all possible subsets (the power set). Note:  The solution set must not contain duplicate subsets. For example, If  nums  =  [1,2,2] , a solution is: [ [2], [1], [1,2,2], [2,2], [1,2], [] ] 3/23/2018 update 一定要把树画全并且标上index。subset和permutation不一样，subset是一直往后走的。 01/22/2018 The i > 0 check is redundant. ------------------------------------ ------------------------------------ ------------------------------------ -------------- 思路： 和subsets完全一样，但要考虑如何去除duplicate。画个图分析下。 上图圈起来的节点就是重复的节点。可以发现，重复的节点和自己的sibling的最后一位是一样的。所以可以在递归循环里面加入：if(nums[i] == nums[i-1] && i!=startIndex ) 判断，是否重复。每一层的第一个节点的最后一位是允许和上一位数重复的。比如这个test case: [1,1]。 实现： search(subset, i+1, res, nums)因为是DFS，递归的时候i+1是为了进入下一层。这道题要首先排序，发重复的数排到一起才能继续往下做。

01/22/2018 Each level add the subset containing its parent node to the result at the beginning.  Have to remove the previous added number, for instance, [1,2], when to go [1.3] needs to remove 2.  Solution: class Solution { public List< List< Integer > > subsets ( int [] nums) { // write your code here List< List< Integer > > res = new ArrayList<> (); if (nums == null) { return null; } //Arrays.sort(nums); List< Integer > subset = new ArrayList< Integer > (); search(subset, 0 , res, nums); return res; } private void search ( List< Integer > subset, int startIndex, List< List< Integer > > res, int [] nums) { res . add( new ArrayList<> (subset)); for ( int i = startIndex; i < nums . length; i ++ ) { subset . add(nums[i]); search(su...

11/30/2017 update 这道题看似简单，但是能写出bug free还有有难度的。 My implementation: ------------------------- class Solution { public int strStr(String haystack, String needle) { if (needle.isEmpty()) return 0; for (int i = 0; i <= haystack.length() - needle.length(); i++) { if (haystack.charAt(i) == needle.charAt(0)) { int temp = i; int j = 1; for (j = 1; j < needle.length(); j++) { if (haystack.charAt(++temp) != needle.charAt(j)) { break; } } if (j == needle.length() ) return i; } } return -1; } } Leetcode clean code hand book has a very genius implementation, I won't be able to reach that level. So skip it. 思路： 太简单了没啥好说的。 实现： corner case不太容易想到，如果对string不熟的话。比如s=“ewffwe”, target=""。这个情况就要返回0。一开始检查corner case代码为： if(source==null||target==null) return -1; if(target.length()==0) return 0;

思路： 马甲题 state: dp[i][j],体积为j时，前i个物品能够占满j体积所需要的方法数。 transition: dp[i][j]+=dp[i-1][j]+dp[i-1][j-k*nums[i-1]], k>=0 && k*nums[i-1]<=j 实现： dp[i][0]需要设置初始值为1，表示体积为0时，前i个物品能取的方法数为1，就是不取。 方法2 ： 用一维数组来做dp[j]=dp[j]+dp[j-nums[i-1]],右边的dp[j]表示前i-1个物品能够取体积为j的方法，因为暂时没有更新。实现的时候是nums[i-1]<=j<=tagert，j是从小到大，因为这道题允许物品重复。在j-nums[i-1]>nums[i-1]这种情况下，dp[j-num[i-1]]就会被更新也就是重复的情况。

思路： state: dp[i][j]，前i个石头，填满体积为j，所获得的最大值。 transition: dp[i][j]=Max(dp[i-1][j-A[i-1]]+V[i-1],dp[i-1][j]), 思维方式和backpack一模一样，就是多考虑了值。 实现： 空间优化，可以用一个一维数组来做。 for(int i=1;i<=A.length;i++) { for(int j=m;j>=A[i-1];j--) { dp[j]=Math.max(dp[j-A[i-1]]+V[i-1],dp[j]); } } 这里第二层循环需要从大到小。dp[j-A[i-1]]其实是用的优化之前上一行的：dp[i-1][j-A[i-1]]。如果从小到大，dp[j-A[i-1]]就会被更新，结果就会出错。

思路： State: dp[i][j]表示前i个石头，能不能恰好装满值j。 Transition: dp[i][j]=dp[i-1][j-A[i-1]] || dp[i-1][j]。这里的思路和house robbery很想，分2种状态，取或者不取i。取i要满足条件，那么前i-1个石头必须填满j-A[i-1]的值。不取i，那么前i-1个石头能够把j填满。 实现： 要检查j-A[i-1]是否大于0，否则会indexoutofbond.